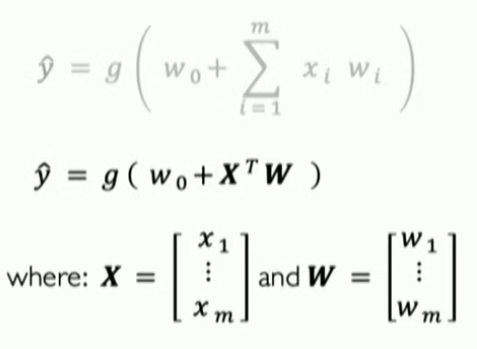introduction to deep learning

VISTA: synthesizing environments for autonomous vehicles to train in
- Don’t have to send the vehicles out into the real world to train; can do so through simulation!
Artificial intelligence (AI): techniques that allow computers to mimic human behavior
Machine learning (ML): train a machine to make decisions based on a set of data, but not explicitly programming it to make decisions
Deep learning (DL): extracting patterns from neural networks to fill in the gaps
- Machine extracts core patterns, then applies it to new data
  - This is as opposed to when humans hand pick and define correct and incorrect data and feed it into a machine to learn (ML)
Perceptron: a single neuron
- Composed of inputs, weights, a bias, nonlinear activation function, and summation
- Steps to get the output of a perceptron ( $\overset{y}{^}$ ):
  1. multiply inputs by weights
  2. sum
  3. add nonlinearity
What is a nonlinear function? Why is it useful?
- What: a function that takes any real number and maps it to a specific range
  - Example: the sigmoid function maps all numbers to be between [0, 1] using the function $g (z) = \frac{1}{1 + e ^{- z}}$
- Why: introduce nonlinearity into the network
Deep neural networks are just neural networks with many hidden layers
Loss functions tell the neural network how big of a mistake it made, given the predicted value and the true value
Loss optimization involves minimizing the loss value — we want to find NN weights that will achieve this
- Gradient descent:
  - For any point, we can compute the gradient of the loss function for that point, and tweak the value such that the loss value decreases
  - Repeat this until convergence to the minimum value
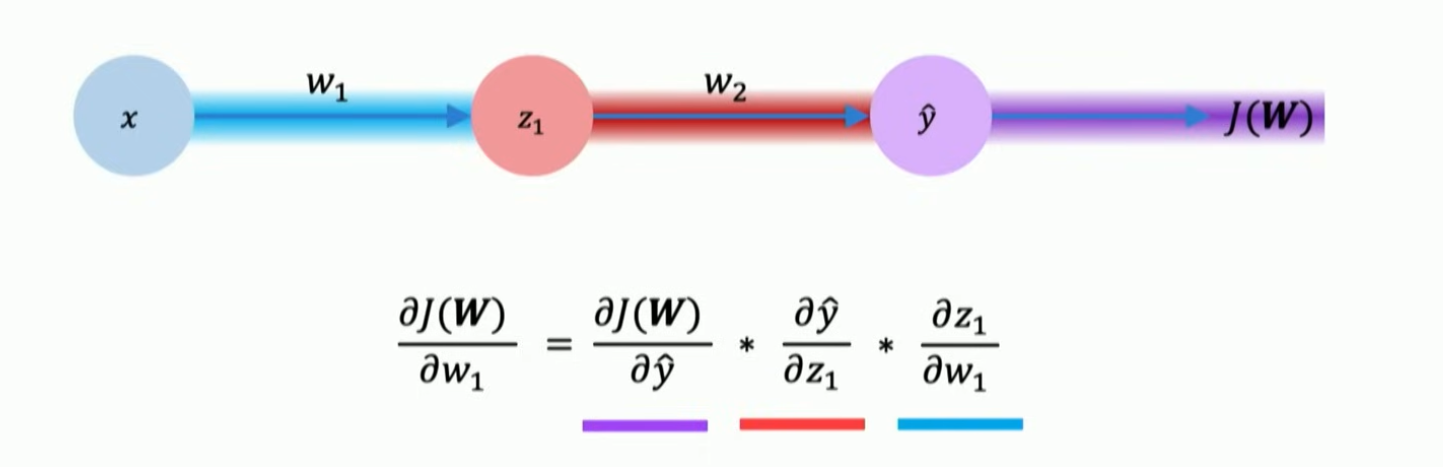
Backpropagation: computing the weight of the node by applying the chain rule on the loss function from the output to the input
Training NNs in practice is difficult
- What is the learning rate? How do we set it?
  - Small LRs converge slowly and occasionally get stuck in local minima
  - Large LRs overshoot and diverge and the NN doesn’t train
  - The learning rate can be an algorithm that adapts to the landscape (possible weights)
- What are batches? Why are they useful?
  - It’s not feasible to compute the gradient over the entire dataset because the dataset is too large
  - Take a small “batch” (sample) of the dataset and compute the gradient over that instead of the entire set or a single point
  - Using mini-batches allows for smoother convergence and faster training (allows for parallelization per batch!!)
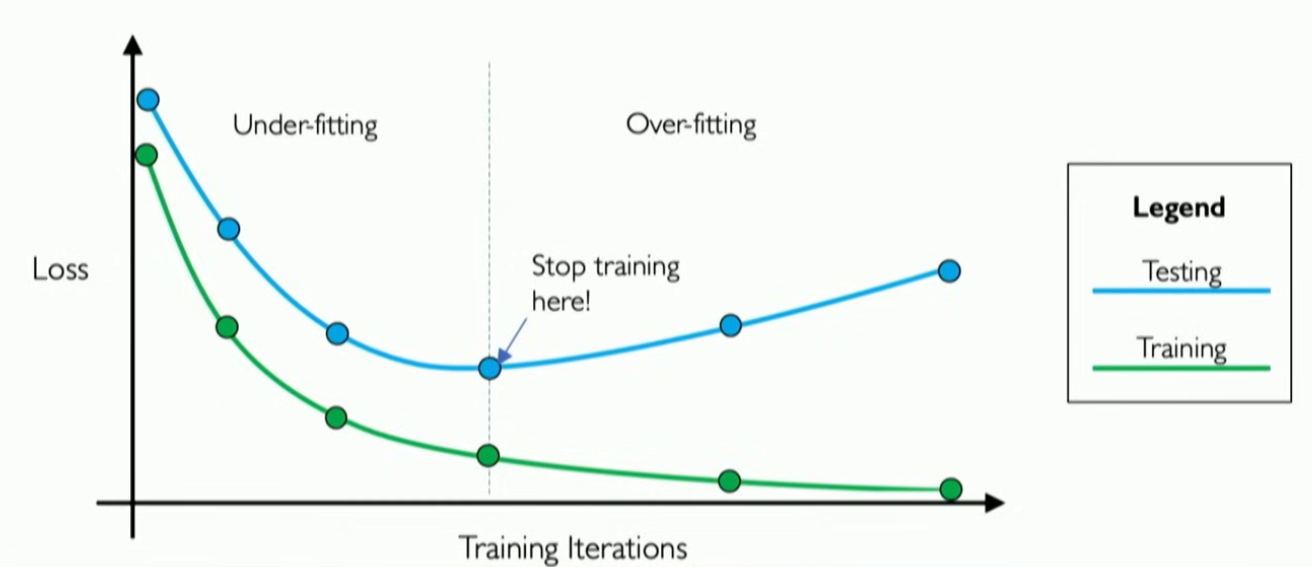
- What is overfitting? How do we correct for it?
  - A model that has overfit to a dataset means it has followed training data too well and can’t generalize to other datasets
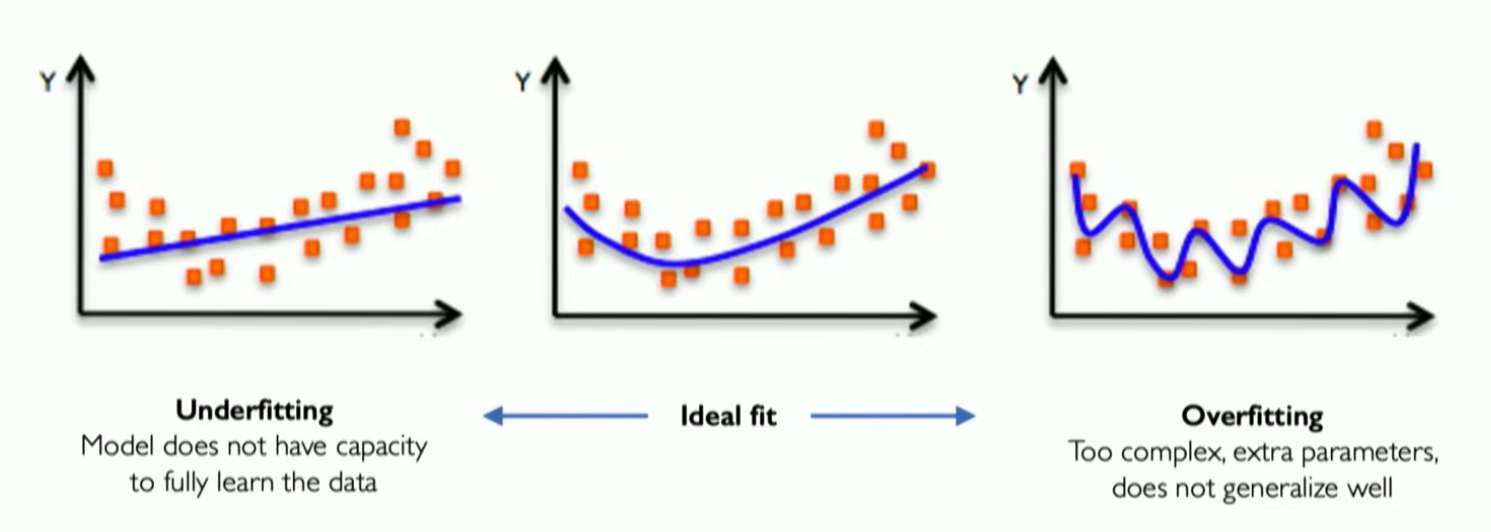
  - Regularization is used to help discourage overfitting and is introduced into the NN
    - Dropout: randomly set some neurons to be 0
    - Early stopping: stop training before the model is good enough to overfit
Summary:
- What is the perceptron? What are its parts? What is a nonlinear activation function and why is it useful?
- How do we get from a single perceptron to a NN? How does the NN learn? What is backpropagation and what is its relation to weight calculation?
- What are some techniques applied in practice that allow for NNs to be accurate?

recurrent neural networks, transformers, and attention

Sequential data are when the points in the dataset depend on other points, for example, sound waves defining audio or a timeseries such as a stock market
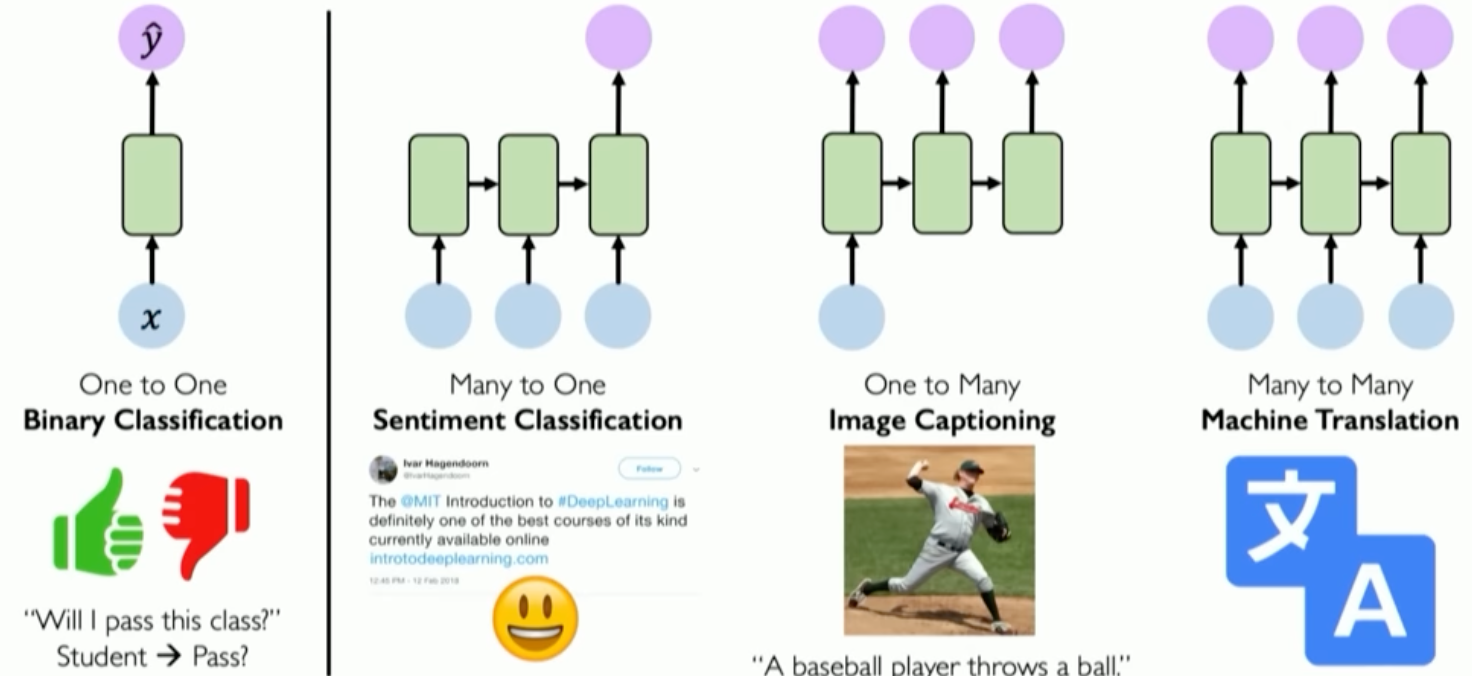
For working with sequential data, we define recurrence relations $h_{t}$ for a time step $t$ which retains information about the state which the NN was in when it produced the output $\overset{y}{^}_{t}$
- Since the state of the NN is tracked for each output, then our output now depends on the state, $\overset{y}{^}_{t} = f (x_{t}, h_{t - 1})$
Formally, recurrent neural networks (RNNs) track state $h_{t}$ which is updated each time step
- Given an input vector, update the hidden state (which has its own weight matrix)
- Then combine the input’s weight matrix and the hidden state’s weight matrix with nonlinearity to get output
- Loss in calculated for each individual timestep and them combined into an overall loss value
- Backpropagation occurs through each individual timestep, then from the current time all the way to the beginning
Issues with backpropagating in RNNs
- Computing the gradient wrt the initial input requires that you perform gradient calculations on many versions of the state weight matrix
- Exploding gradients > gradient clipping
  - Gradients keep increasing and get extremely large
  - Scale back large gradients by clipping
- Vanishing gradients
  - Harder time capturing long term dependencies because many small numbers are being multiplied together
  1. Activation function tweaking
  2. Parameter initialization via setting weights to identity matrices
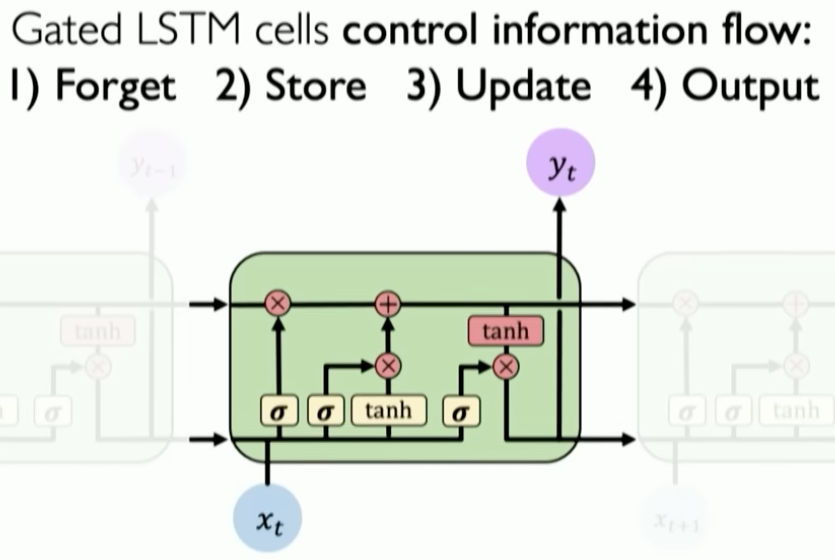
  3. Gated cells: using gates to filter information per recurrent unit (LSTM)
What should we keep in mind when designing models for sequences?
- Variable-length of the sequences
- Dependencies between data points that are distant from each other
- Maintaining order
- One set of weights can be applied to any timestep input and still work
Encoding language for NNs: transform words into vector representations
- One-hot embedding
  1. Obtain a vocabulary (corpus)
  2. Map each word to an index
  3. A word is a vector of 0s with a 1 at the word’s index
- Cons to one-hot embedding: the words have no meaning to each other
- Learned embedding: use a NN to learn an embedding
Limitations of RNNs in application
- Encoding bottlenecks: in the case of many-to-one models (sentiment classification), how do we encode all the text to just one single result without losing information?
- Slow: can’t parallelize because every step depends on the previous one
- No long term memory
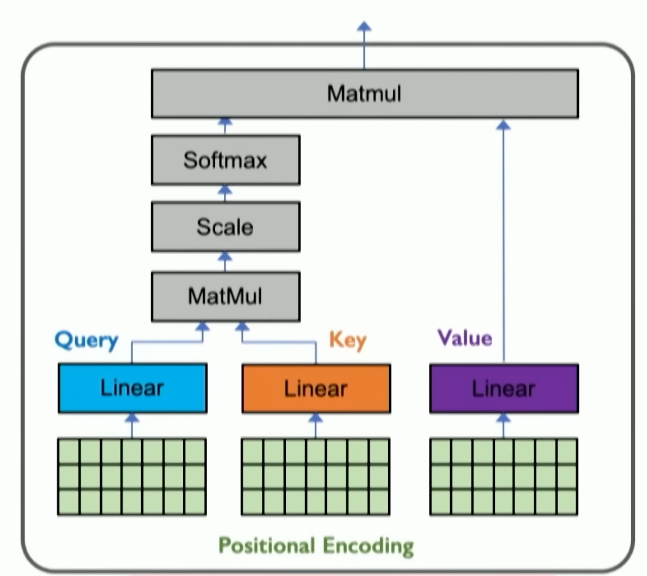
Attention: how can we eliminate the need for recurrence and improve on the above issues, but still analyze data in sequential order?
- Identify the most important features in the input
  1. Encode position information (embedding)
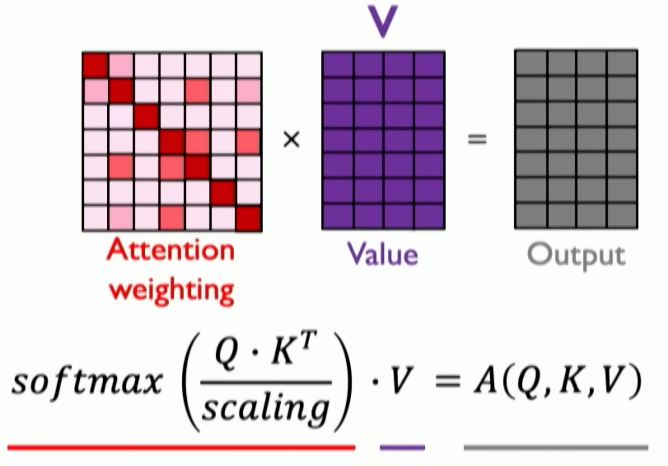
  2. Extract query, key, value for search — what is the most important information related to my request?
  3. Compute attention weighing — compute pairwise similarity between each query and key
    - How similar are any two features?
    - Computed using the dot product between query and key, called the cosine similarity or the similarity metric
  4. Extract features with high attention
Summary:
- What are RNNs? What are its key features? What are they useful for?
- How do RNNs perform backpropagation and what are some major issues of backpropagating in RNNs? What are some downsides of RNNs?
- What is attention? What is its importance with relation to RNNs? Why is it important?